数値計算(量子ゲート方式)
概要
既存の古典コンピュータ、量子コンピュータのそれぞれの特性を組み合わせた数値計算の提案を行っています。
事例1(多質点系の強制振動)
多質点系の強制振動(用語1)の動的シミュレーションに対して、 運動方程式の離散化の際に現れる線形方程式の求解に、量子アルゴリズムであるHHLアルゴリズム(用語2)を適用しました。 結果として、HHLアルゴリズムでも実用上問題ない精度で解を求めることに成功しました。
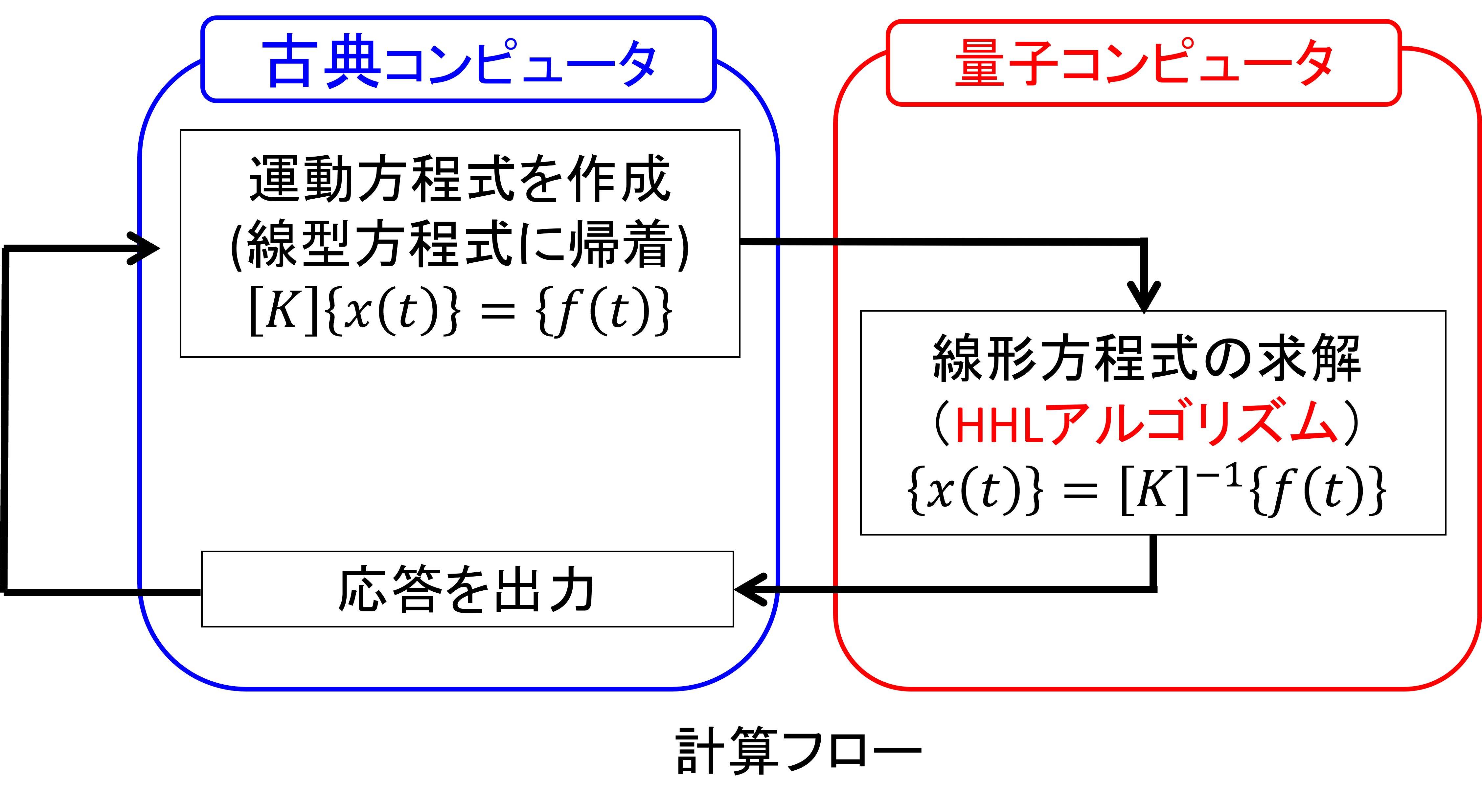
シミュレーションシステム
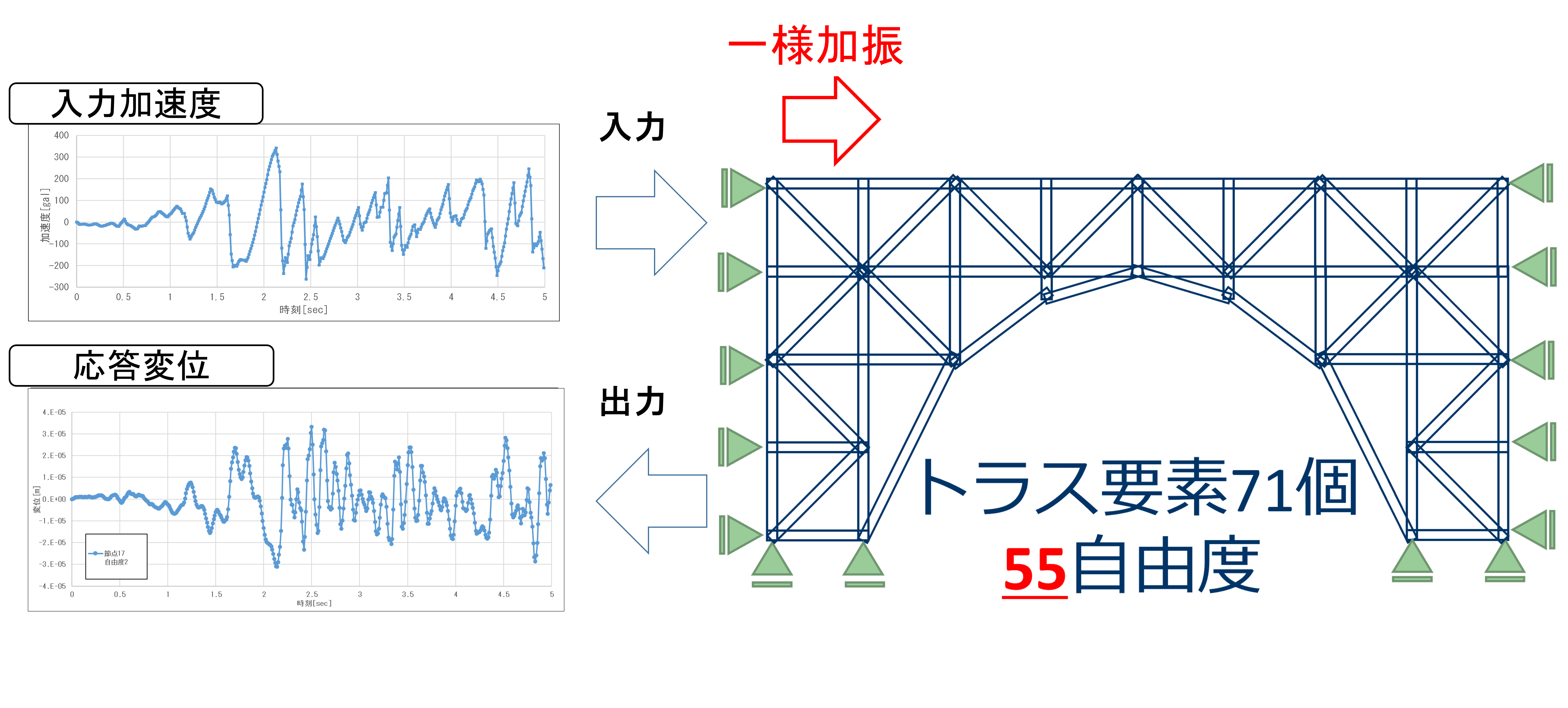
55自由度トラスモデルと入出力
強制振動シミュレーションの結果動画
用語1 : 強制振動
強制振動とは、毎時刻外部から力が働き、一定の運動をし続けるものをいいます。
例えば、ブランコを背中から押してもらう場合や、水晶振動子を電気で振動させる場合(腕時計のクォーツや、パソコンのクロック発振器)です。
用語2 : HHLアルゴリズム
量子コンピュータは、固有値計算が得意なため、固有値を使って線型方程式を解くアルゴリズム(Harrow-Hassidim-Lloydアルゴリズム。以下、HHLアルゴリズム)に着目しました。
本アルゴリズムは、係数行列がエルミート行列である場合に対して、逆行列計算を効率的に行うことができる量子アルゴリズムです。
疎な連立一次方程式の解法に使用されるため、数値解析や機械学習などあらゆる分野への応用が期待できます。

HHLアルゴリズムを実現する量子回路
事例2(キャビティ流れ)
計算モデル
2次元キャビティ流れ(注意1)は、流体シミュレーションのベンチマーク問題としてよく知られています。 下の図に示すように、キャビティ流れの計算領域は、天蓋を除いた3辺が壁に囲まれた正方形領域であり、天蓋部分の辺境界ではせん断流速が与えられます。 このせん断流速により内部の流体が駆動されて回転流が発生します。
離散化手法としてはSMAC法(Simplified MAC method)を採用しました。 SMAC法では圧力分布を求めるのに圧力ポアソン方程式を解く必要があり、この求解処理にHHLアルゴリズムを適用しました。 計算システムに対するHHLアルゴリズムの適用方法は、事例1(多質点系の強制振動)と同様です。
また、今回は計算格子として等間隔構造格子を採用して、流速と圧力定義点の配置はスタガード格子を採用しています。
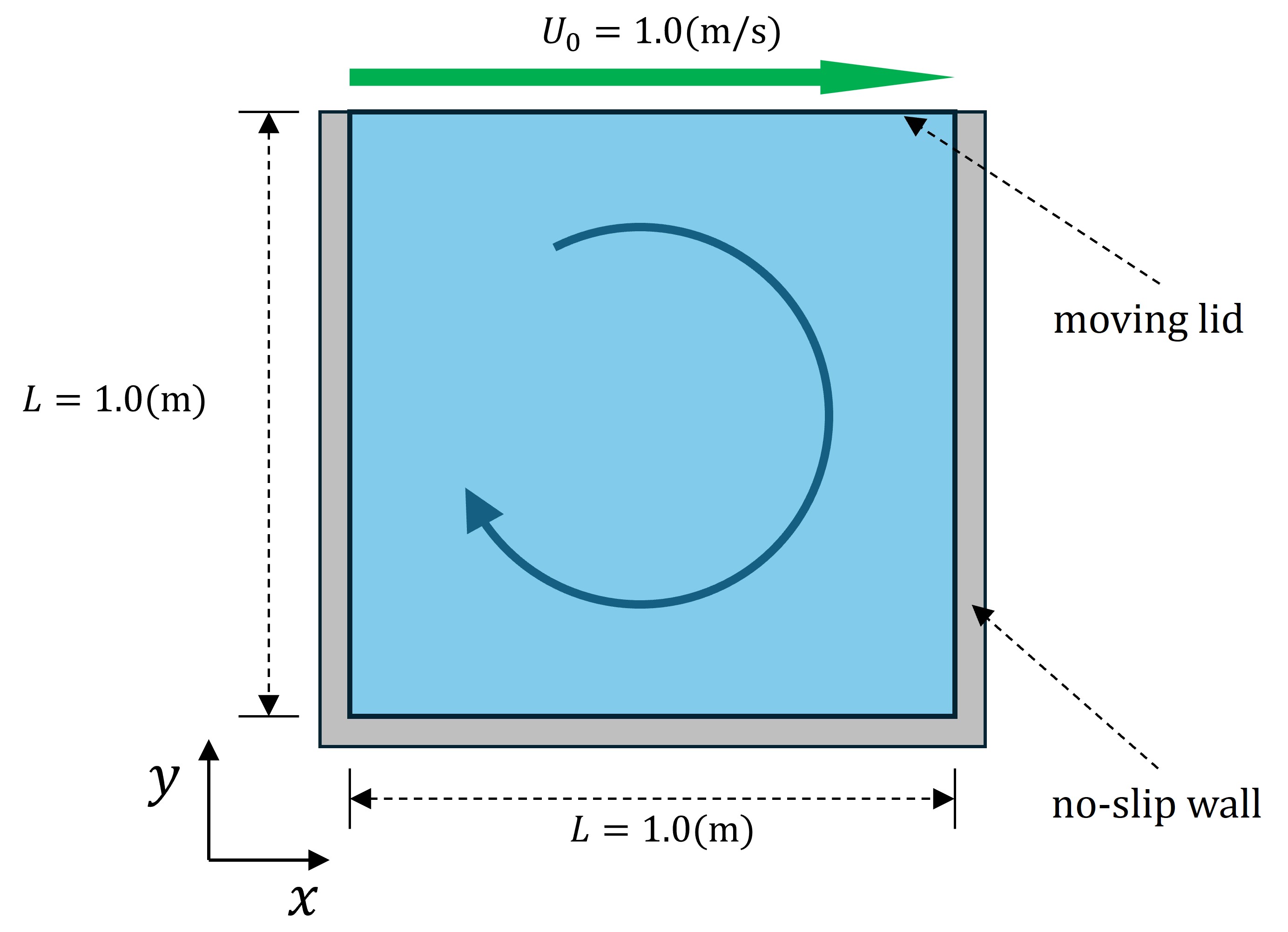
2次元キャビティ流れ
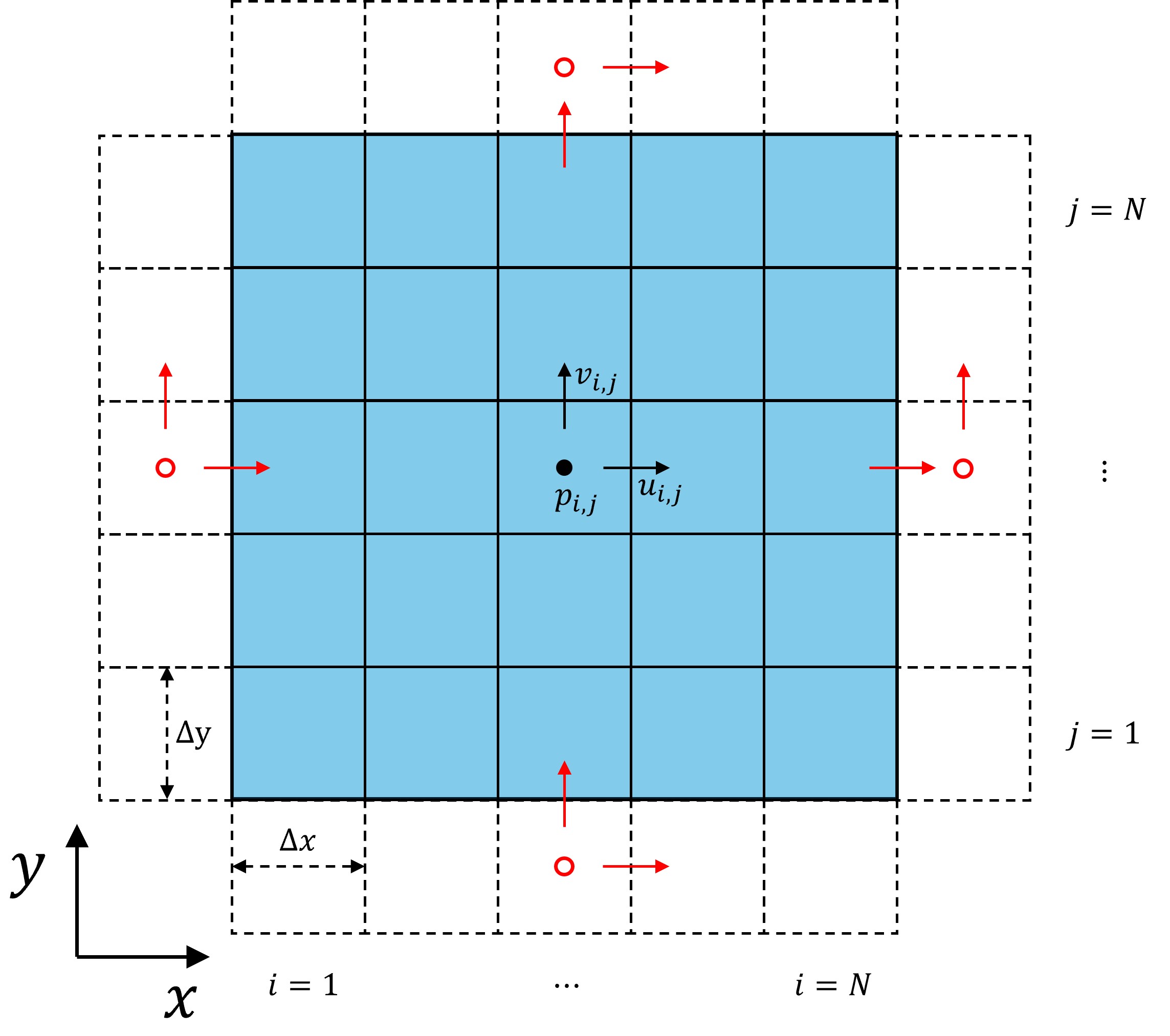
構造格子(等間隔)
HHLアルゴリズムによる計算
ここでは、量子アルゴリズム(HHL)を使ってキャビティ流れを計算した結果を示します。 ただし、格子解像度はNx=Ny=8と設定して、計算点数が少ないモデルを対象としました。 計算結果として、流速分布と圧力分布を下図に示します。 結果の比較のために、それぞれの分布について古典計算で得られた結果も並べて表示しています。 古典計算の結果は、圧力ポアソン方程式の求解処理にNumpyが提供する線形方程式ソルバーを利用しています(NumpyはPythonの標準ライブラリです)。 結果として、両者の結果は概ね一致しており、流体シミュレーションでもHHLアルゴリズムを活用できることが期待できます。
流速(Re=1000, Nx=8, Ny=8)
左図:量子アルゴリズム(HHL)
右図:古典アルゴリズム(Numpy)
圧力(Re=1000, Nx=8, Ny=8)
左図:量子アルゴリズム(HHL)
右図:古典アルゴリズム(Numpy)
注意1 : キャビティ流れ
キャビティ流れの計算について、格子解像度をNx=Ny=50とした時の流速分布(Re=1000)を下図に示します。
領域下部の左右の端に二次渦の発生が確認できます。
この結果は古典コンピュータで計算したものです。
つまり、HHLアルゴリズムは使わず、標準的な手法(SOR法)で圧力ポアソン方程式を解いています。
将来的に、量子コンピュータ技術が発展した先で、このような規模のモデルも量子アルゴリズムによって高速に計算できるようになることを期待しています。
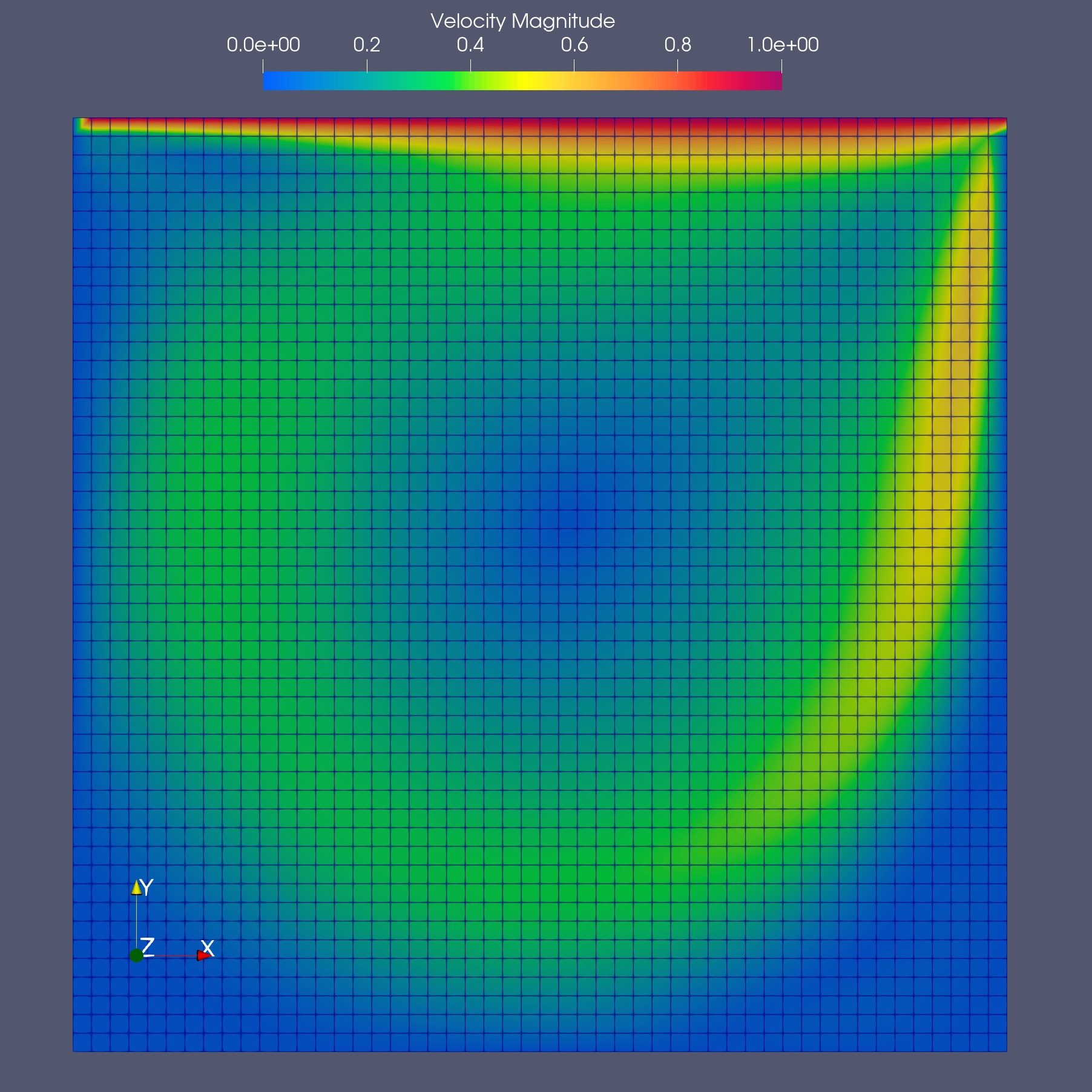
計算格子(Re=1000, Nx=50, Ny=50)
※古典計算(SOR法)を利用
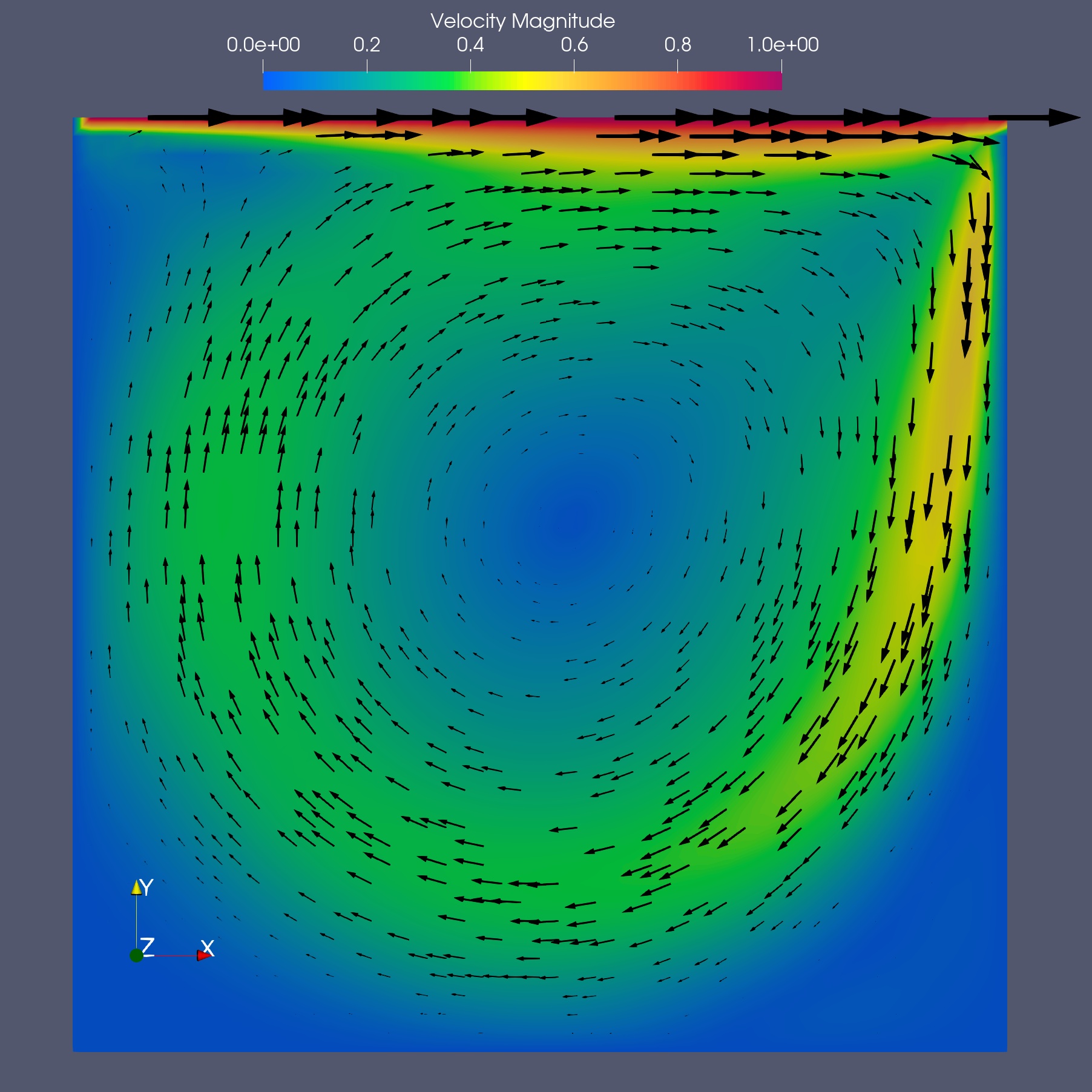
流速(Re=1000, Nx=50, Ny=50)
※古典計算(SOR法)を利用
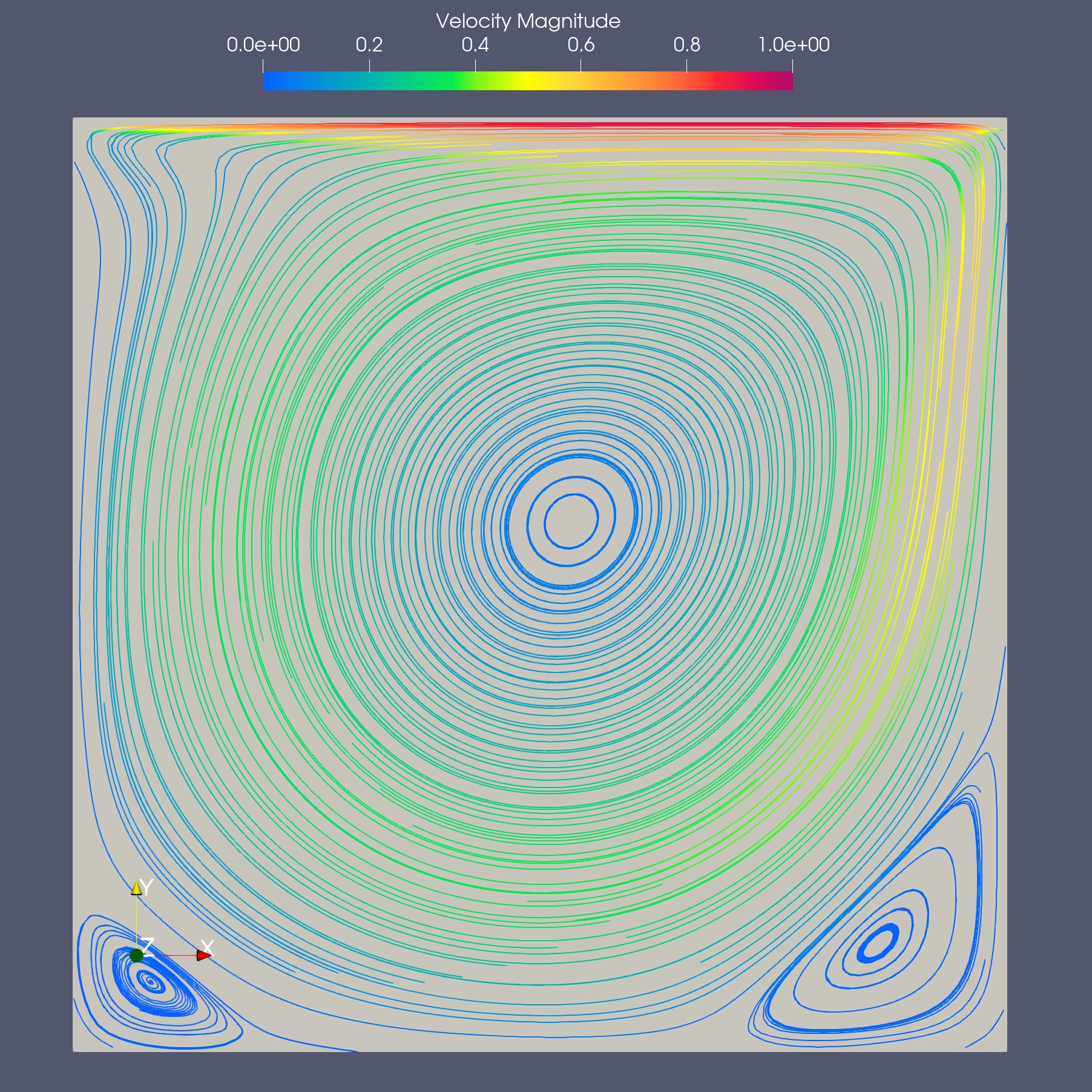
流線(Re=1000, Nx=50, Ny=50)
※古典計算(SOR法)を利用
補足
【システム構成】
- OS:Windows
【開発ツール】
- Python
- Qiskit
【対象業務】
- 概念実証(社内研究)
【参考】
本ページの事例1の内容はInterface誌(CQ出版)の2022年6月号に掲載されました。記事の原文を提供可能です。希望される方は、以下のお問合せフォームよりご連絡下さい。

Interface誌(CQ出版)の2022年6月号
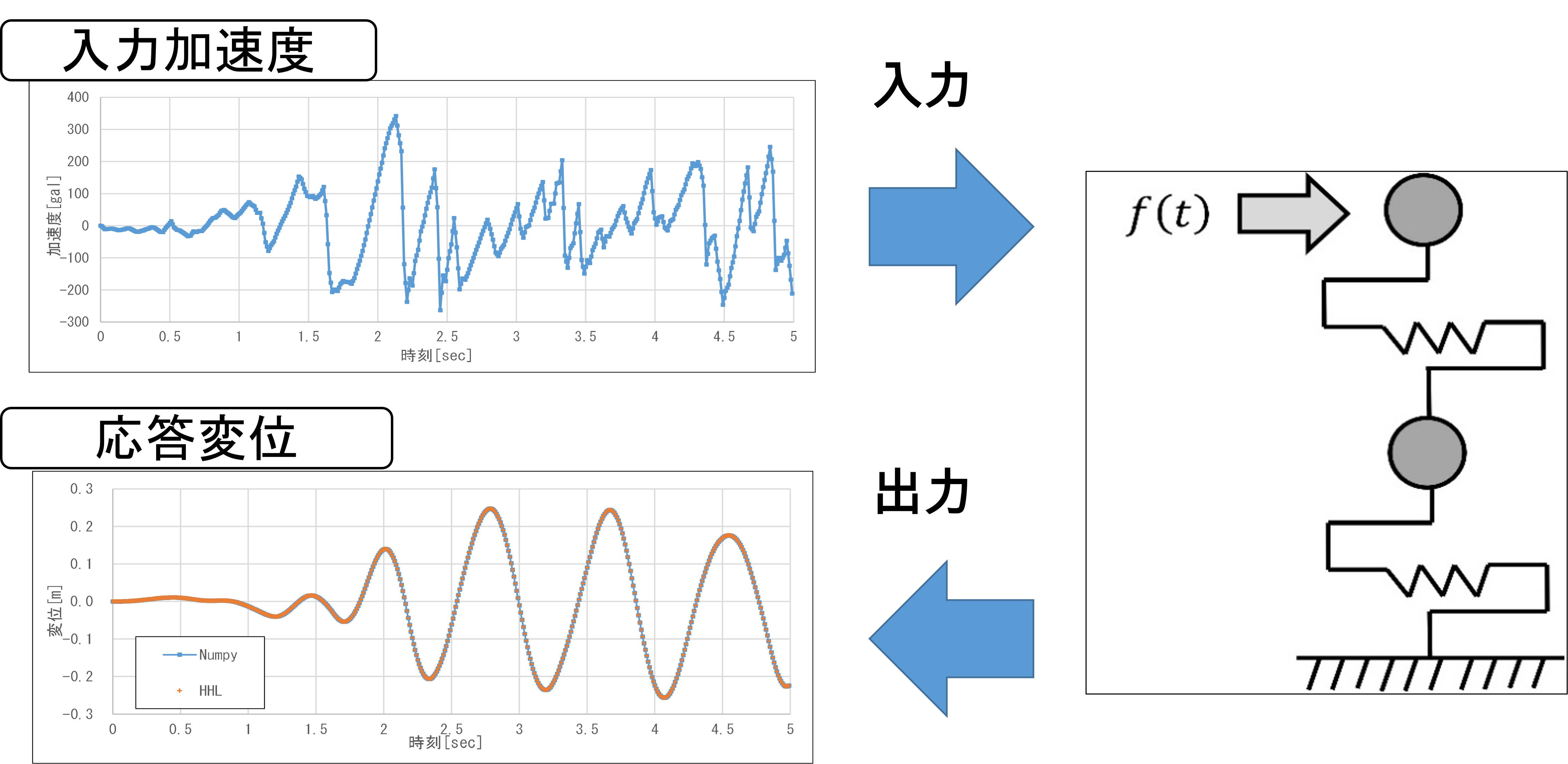
2質点系バネモデルと入出力